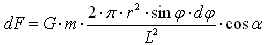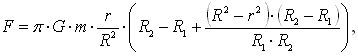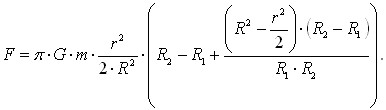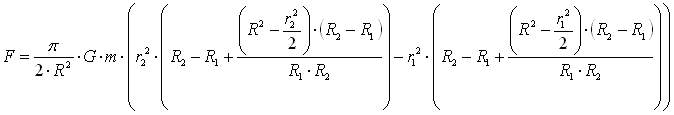Гравитация во вселенной (часть 2) | 23:54 |
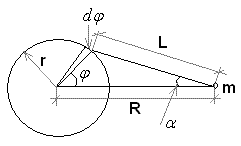
Гравитация во вселенной. Часть 2. В прошлый раз нам не удалось получить явной формулы для шара. Сейчас мы вернёмся к этой и другим задачам, использую другую методику. Задача 1. Рассматривается тело массой m расположенное на расстоянии R от центра сферы, радиуса r. Сфера имеет плотность равную 1.
Решение будем строить следующим образом. На сфере вырезается круг
шириной Масса, вырезаемого круга будет:
Расстояние до любого элемента этого круга от нашего тела будет L.. Далее все определения должны быть понятны из рисунка.
Справедливы следующие равенства: 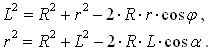 Дифференцируя первое равенство, получаем: 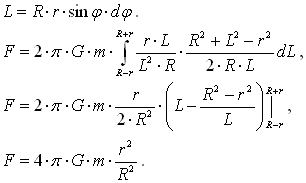 Эта формула ничем не отличается от стандартной формулы. Задача 2. Задача, аналогичная предыдущей, только, рассматривается часть сферы.
Задача 3. Теперь рассматриваем тело и шар. 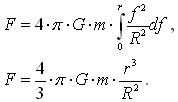 Формула не отличается от стандартной. Задача 4. Задача аналогичная предыдущей, только рассматривается полый шар. 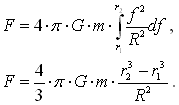 Задача 5. Задача аналогична задаче 3, но рассматривается часть шара.
Задача 6. Теперь рассматриваем часть полой сферы.
Задача 7. Аналогичные задачи можно рассмотреть для эллипсоида. Я думаю, что здесь не должно быть трудностей. Зависимости несколько усложняться, но в целом интегралы берутся. Как быть, если предмет находится по отношению к телу не симметрично? Как быть, если само тело представляет собой не точечный источник? Эти вопросы мы рассмотрим в следующих статьях.rznusl.ucoz.ru © 2011 | |
| Категория: Мои статьи. | Просмотров: 1794 | Добавил: rznusl | Рейтинг: 5.0/2 | | |
| Всего комментариев: 5 | ||||||
| ||||||
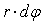 .
.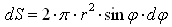 .
.