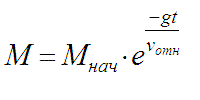Александр Ильич Митькин

(Рязань, статья 2006 г - печаталась в одном  из рязанских журналов)

 Хочу предложить на рассмотрение мою статью ,возможно это поможет в создании эффективного махолёта .

Возможно мои расчёты были неверны ,но если кого-то заинтересует я могу их полностью привести .(выполнял так же и для атмосферы - много вычислений,  дважды делал полный расчёт - результаты не сошлись, но выгода в обоих случаях была)

Как повысить КПД летательного аппарата

   Речь пойдёт о полётах летательных аппаратов над поверхностью планеты (например Луны) в безвоздушном пространстве и на малых скоростях.

Рассматривая полёт в безвоздушном пространстве над планетой, мы можем полное движение разбить на две составляющие:

1)     движение вдоль поверхности (горизонтальное);

2)     движение по вертикали (либо борьба с силой тяжести, если движения нет. Ведь скорость малая и, следовательно, центробежную силу мы не учитываем. ).

Соответственно мы можем отдельно рассмотреть и затраты на эти две составляющие.

Рассмотрим движение по вертикали. В безвоздушном пространстве его описывает уравнение Мещёрского следующего вида:

Mvˈ=Mˈvотн+F, где М – масса аппарата, v – скорость аппарата, F – внешняя сила (сила тяжести).

vˈ=g – ускорение свободного падения,

vотн≈4000м/с – скорость истечения газов (значительное увеличение этой скорости решило бы проблему полётов человека к другим планетам).

Если тело не совершает вертикальных перемещений, т.е. оно летит горизонтально, то получаем уравнение:

0=Mˈvотн+Mg ⑴

Решением его будет

, где t – время.

Допустим теперь, что тело периодически совершает движения по вертикали (подымается с ускорением a и падает с ускорением g. Т.е. полёт проходит по волнистой траектории ). Подъём аппарата описывает следующее уравнение:

Mvˈ=Ma=Mˈvотн+Mg ⑵

Пусть t1 – время подъёма аппарата, t2 – время падения аппарата, h – высота подъёма (падения) аппарата, т.е. амплитуда колебаний.

Получаем h=a(t1)²/2=g(t2)²/2. t3=t1+t2 – время совершения одного колебания.

Думаю нет необходимости привести решение уравнения ⑵.

Будет ли расход горючего в этом случае меньше, чем при полёте по горизонтали?