Не так давно мне поступило предложение рассчитать створку (заказчик: Serguei Pevzner <start@centrale.ru>). Суть заключается в том, что створки располагаются по кругу, а их раскрытие выглядит так, будто отверстие расширяется в сторону – как в фантастических фильмах.

   Идея мне показалась интересной и не совсем правдоподобной. В Интернете я ничего по этой теме не нашёл, т.к. названия системы у меня нет. Заказчик же сказал, что, возможно, делали в каменном веке – может, пошутил.

   В общем, я взялся.

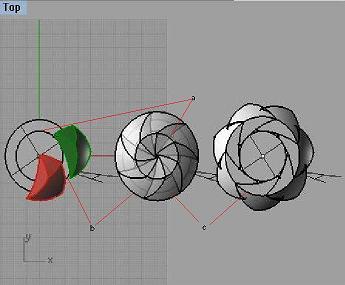
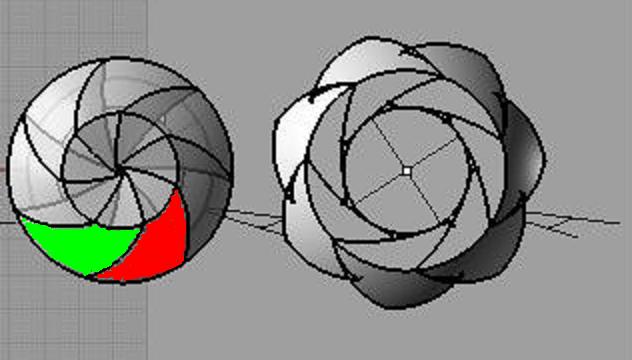
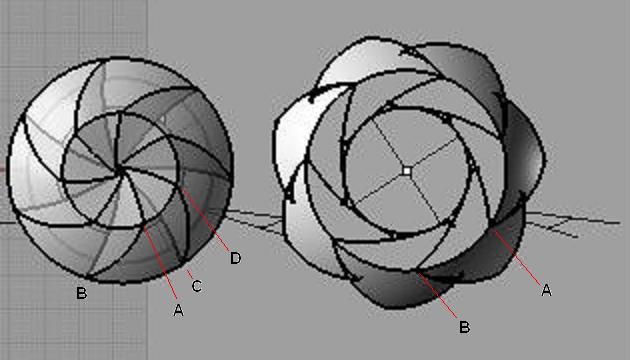
   Вскоре, я определился с тем, как строятся подобные поверхности. Кроме того, я пришёл к выводу, что, да – в каменном веке такую штуку вполне могли сделать.

    Я рассмотрел, только внешнюю часть створке. Но для понимания подхода, думаю, этого достаточно.

   Суть построения такая (см. рисунок). При повороте красной и зелёной створок на некоторый угол (для каждой створки своя точка, вокруг которой она вертится) точка В, принадлежащая, красной створке, будет соприкасаться с некоторой точкой Т, принадлежащей зелёной створке. Чтобы определить, где была точка Т в начальный момент, мы должны зелёную створку повернуть обратно (на тот же угол). Таким образом, зная поворот (положение точки В в любой момент времени), мы однозначно определим некоторую линию на поверхности зелёной створки (описываемой точкой Т). Дуга же ВА определит некоторую поверхность на зелёной створке. Далее, эта поверхность определит левую часть красной створки; излишки убираются, т.к. примыкание (отсутствие щели) обеспечивает, уже, дуга, ВА. Таким образом, решение возможно всегда и оно единственное. Надо только задать начальное и конечное положение створок.

   Такой путь правилен, но не оптимален – в каменном веке так бы не делали. Существует более простой подход.

   Я сделал расчёт не для 6 створок, как на рисунке, а для 3-х. Оказалось, что линия, соответствующая точкам Т, есть сечение поверхности тора. Построив эту линию, мы будем прикладывать к ней дугу ВА (лекало). Нам известно положение этого лекало, относительно построенной линии, поэтому это всегда сделать можно. Вот и вся идея построения внешней части створки.

   Далее я приведу свои расчёты, чтобы вы могли сами в них разобраться. Но прежде должен сказать, что я поворот фигуры в пространстве рассматриваю как два поворота – поворот вокруг вертикальной и поворот вокруг горизонтальной оси (в общем случае углы поворотов разные). Кроме того, я взял наиболее удобный случай. Соответственно круг имеет радиус равный 1.

   Я рассматриваю проекцию линии, вырисовываемую точками Т на вертикальную и горизонтальную плоскости. Вертикальная плоскость перпендикулярна горизонтальной оси вращения.

   Горизонтальная ось.

http://rznusl.ucoz.ru/stati/stvorka/q1.jpg

   Вертикальная ось.